3. Photometry
Pierre Hily-Blant
Université Grenoble Alpes // 2020-21 (All lectures here)
1 Introduction
- This chapter will deal with photometry, that is, the art of converting a measurement such as elecron/s or photons/s into a physical SI unit such as W m-2 Hz-1
- Motivations underlying photometry are multiple, from the simple need to understand how stars span a broad range of apparent magnitude, shine reddish or blueish, etc., to the quest for precision and accuracy in measuring the universe.
- Historically, photometry started with stars, for quite obvious
reasons. Actually, understanding the birth, evolution, and fate,
of stars is central to astrophysics for many reasons.
- We may perhaps summarize that stars are the chemical factories of the universe since they synthesize the stable heavy elements beyond those produced by the Big Bang, such as carbon, oxygen, nitrogen, and their isotopologues.
- And also, galaxy evolution is largely driven by stars through their feedback (fountains, cosmic rays, etc).
- Indeed, deriving stellar properties (mass, size, composition, internal motions and state, magnetic fields) is a major task of astronomy and astrophysics for decades, trying to combine theory and observations into a comprehensive understanding of stellar structure and evolution.
- In this chapter, we shall not discuss stellar structure but rather use the properties of the stars to measure distances on a wide range of scales. As such, stars can tell us about the structure of our galaxy and similar ones. Moreover, the brightest stars (e.g. SNe Ia) can be observed up to redshifts ∼ 2 and therefore provide ways to measure the universe.
- In this lecture, you may learn about:
- Empirical knowledge of stars:
- spectral and luminosity classification; classifying the stellar ecosystem
- Fundamentals of radiation and photometry:
- Apparent and absolute magnitudes
- Photometric systems (filters, zero-points)
- Bolometric correction
- Extinction correction and interstellar reddening
- How we can measure distances beyond the parallax limit using standard candles
- Empirical knowledge of stars:
2 The Classification of Stars
Observed properties of stars: spectra

- A-type star: strong and broad H absorption lines
- G-type star (like the Sun): many lines (ionized and neutral atoms)
- M-star: strong molecular bands (e.g. TiO)
Stellar spectra

- Note: our ability to detect absorption lines depend on the background intensity: strong background allow weak absorption lines to be detected (see radiative transfer lectures)
2.1 The spectral classification of stars
The spectral classification of stars
- Harvard spectral taxonomy in the 1890s: O B A F G K M (if you need
this: Oh Be A Fine Guy/Girl Kiss Me)
- The strange choice and ordering of the letters is due to historical reasons: starting from an alphabetic order (A, B, C, etc), the order and retained letters had to adapt to the continuously evolving picture; eventually, no logic is apparent in the final list.
- Numerical subdivision: O0-9 B0-9 etc
- Vocabulary: early K type is K0, late G star is B9
- Harvard classification: empirical (based on some key lines,
e.g. HeI, HeII, CaII, FeI, etc)
- Note: spectroscopic notation HeI stems for neutral He, HeII for He+, CaII for Ca+, etc
- Balmer lines (n=2) are maximum for A0 (Teff = 9520 K)
- HeI are strongest for B2 (Teff = 22000 K)
- the CaII doublet (H line at λ=396.8 nm and the K line at λ=393.3 nm) are strongest for K0 (Teff= 5250 K)
- spectral type based on absorption line ratios
- Catalogues: Henry Draper Catalogue (HDxxxxx) (225,300 spectra classified by Annie J. Cannon, between 1911 and 1914)
The Harvard College Observatory group

At the Harvard College Observatory, in 1892, a group of women, led by Williamina P. Fleming (standing middle rear), Henrietta S. Leavitt (fourth from left, sitting), and Annie Jump Cannon (far right), in the group of Edward Pickering (rear left).
Example of stellar spectra

Note the clear difference between A-type stars (left) showing few, isolated, deep lines, and late types (G, K, M) stars (right), showing more complex spectra with weaker lines.
The O-B main sequence: examples

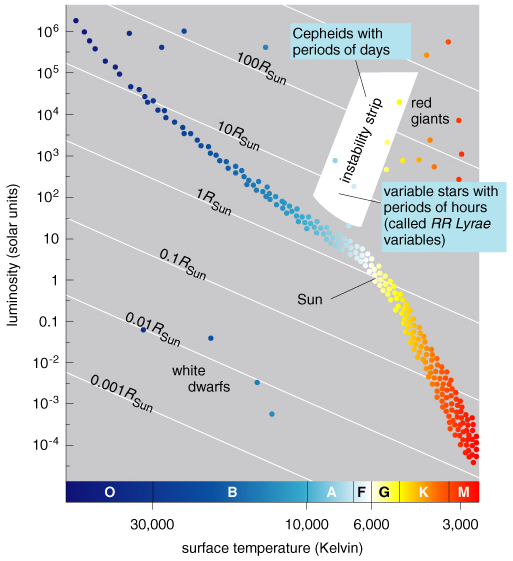
- Useful ressources: Atlas of stellar spectra (MKK), SDSS stellar spectra
- The spectral classification more or less reflects the effective temperature of the star, with O stars being the hottest/bluest, and the M dwarfs being the coldest/redest.
The spectral classification of stars
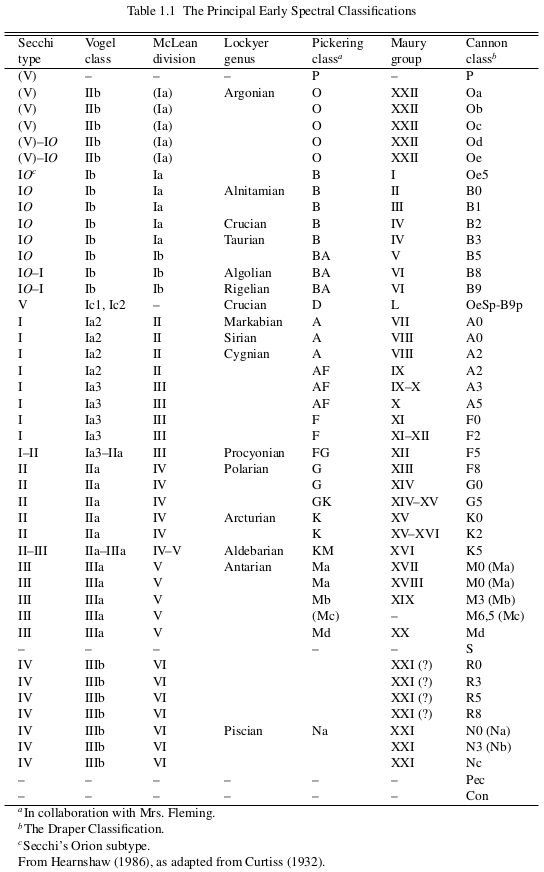
- Several groups, several systems, several variables
- The 1912 Draper Catalogue of Stellar Spectra (essentially by Annie J. Cannon) was validated by an international Committee.
- Henry N. Russell supported the non-alphabetical order of the letters: "This helps to keep the novice from thinking that it is based on some theory of evolution." Actually this is for historical reasons, with the letter ordering and choice evolving with the diversity of stellar spectra.
- Karl Schwarshild recommended to keep as little variables as possible: "ultimately the spectrum of a star might depend on nothing other than its mass, its age and its temperature"
- Annie J. Cannon pursued the work, culminating in the Henry Draper (HD) catalogue finally published in 1924 (1USD per star).
2.2 From the Harvard to the Morgan-Keenan (MK) classification
Luminosity class
- At the same period at which the spectral classification was set up, Antonia Maury (another woman of the Harvard group) introduced an idea at the basis of what was later called the luminosity class. The basic observational fact is that stars of a given spectral class could have lines with different width and strength
Example of luminosity effects at A0
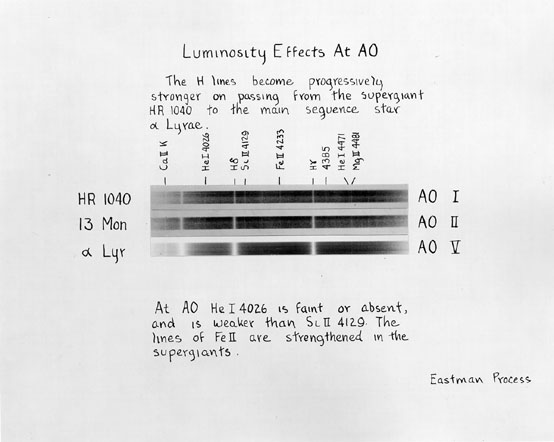
Limitations of the Harvard classification
- The spectral classification does not reflect the origin of
stellar spectra
- Example: Hydrogen lines in Vega (A0 by definition) are much stronger that in the Sun (G2); but Ca lines are much stronger in the Sun than in Vega
- Origin: Teff ? (9500 K for Vega, 5777 K for the Sun); chemical composition ?
- As mentioned earlier, the Harvard classification is empirical. In particular, it is biased towards the lines in the visible; but what about other spectral ranges (IR, UV) ?
- Later on, the discovery of low-Teff stars in SDSS (Sloan Digital
Sky Survey) and the 2MASS (2-Micron All-Sky Survey) could not fit
into this classification, and new spectral types were added:
L-type (Teff=1300 to 2500 K) and T-type (Teff<1300 K)
- Brown dwarfs (deuterium-burning during contraction, but threshold for H-burning never reached)
Which quantity to classify stars ?
- Harvard classification: empirical, essentially based on Teff
- But two stars with the same Teff can have different luminosity
Underlying physical questions
- What causes the spectrum of a star: Teff, chemical composition?
- Answers: both, and even more
- chemical composition
- physical state (convection zone)
- radiative transfer with quantum mechanical description of ligth/matter interactions (emission, absorption by atoms)
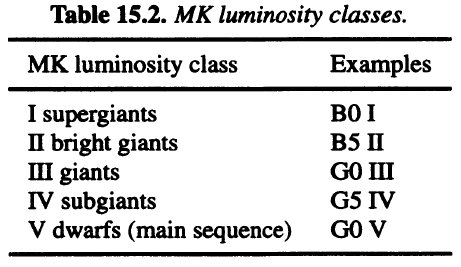
Luminosity classes in the MK classification
- Not adopted in Harvard classification
- Extended in the MK (Morgan and Keenen) classification
- Luminosity classes
- I, Ia, Ib, have very narrow, very weak lines: supergiants
- II and III have narrow, weak lines: giants
- IV has intermediate lines: subgiants
- V has very strong, broad lines: dwarfs
- Modern notaion for Spectral types:
- α Lyr: A0 Va
- Type: A
- Subtype: 0 to 9, 0 being the hottest
- Luminosity class: I to V, I being the largest
- The Sun is G2 V in MK classification

3 Magnitudes and photometry
- What we will learn
- apparent magnitude m and flux density Fν (or Fλ)
- absolute magnitude M and luminosity Lν
- bolometric magnitude and flux F
- bolometric correction: from F to L
3.1 Apparent magnitudes
- Visual magnitude \(m\) describes the "brightness" of a star
- Classification by Hipparchus (190-120 BC) of ∼800 stars,
further complemented by Ptolemy (150) three centuries later (∼
1000 stars);
- \(m=1\): brightest stars
- \(m=6\): faintest stars to the naked eye (and w/ dark sky; will there still be any dark place on Earth in a century from now?)
- Note: Brightest star is the Sun: mV=-26.7; next one is Sirius (Canis Major), mV=-1.5;
Magnitude is a relative measurement (Note: log means log10 ≠ ln, unless stated otherwise):
\[ m_2-m_1 = -2.5\log (N_2/N_1), \quad N_2/N_1= 10^{(m_1-m_2)/5} \]
where \(N(\nu)\) is the photon rate detected over a spectral interval around a given wavelength
- A difference of 5 magnitudes corresponds to a factor 100 in brightness.
Magnitude, flux density, and photon rate
- There is no unique definition of the apparent magnitude.
- The definition depends on the device used to measure the magnitude:
- energy integrating devices (such as photomultiplier tubes) are sensitive to the energy, hence to the flux density Fν
for such devices, the magnitude would be defined as
m2-m1 = -2.5log (F2/F1)
- most modern detectors are photon-counting detectors: they are sensitive to N=Fν/hν.
- In both cases, the apparent magnitude \(m\) is related to the flux density Fν
- The monochromatic flux density Fν (to be defined in the next Section) is a quantity that describes the amount of energy received from a source by an observer, per unit area at the observer location; its units are W/m2/Hz or W/m2/m;
- The total, or integrated, flux density is ∫ Fν dν.
- Important: the flux density decreases as d2, where d is the distance between the source and the observer.
3.2 Absolute magnitudes
- Definition: the absolute magnitude M of a source is the apparent magnitude m of that source if it was moved to a reference distance d0=10 pc (chosen by convention)
Geometrical dilution of the flux: Fν(d)∝ d-2: F10pc = Fmeasured x (d/10pc)2; taking the -2.5log(F) gives:
M = m + 5 - 5log(dpc)
Definition of the distance modulus:
DM = 5 log(dpc)-5 = 5 log(d/10 pc), dpc/10 = 10(DM/5)
Apparent vs absolute magnitude:
m = M + DM, M=m-DM
- Stars with d>10pc (32.6 ly) are brighter than they appear: DM>0, M<m
- Example: DM of M31 is 24.4 mag, d≈ 1 Mpc; an MV=5mag star placed in M31 would have an apparent magnitude V≈30;
3.3 Filters, photometric systems, and photon rate
- Nowdays, photometry is performed with photon-counting detectors, which measure the photon rate N; such a detector is placed behind a filter
- Filters are defined by transmission function: R(λ)
- normalized response function: Rmax = 1
- effective wavelength = <λ> (1st order moment=R-weighted average)
- integrated area (or surface): S=∫ R(λ) dλ
- effective bandpass in the Gaussian approx.: Δλ = 2σ (σ=2nd order moment)
- A set of filters covering the range from IR to UV defines a photometric system
- One must also take into account the efficiency of the detector: η(λ)≤1
- In a given filter, the photon rate is \[ N = \int R(\lambda) \eta(\lambda) F(\lambda) \frac{\lambda}{hc} d\lambda \]
Various photometric systems

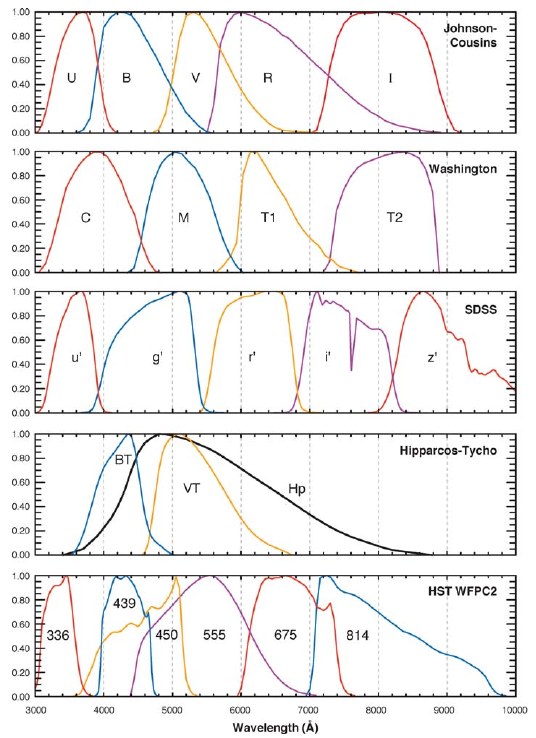
- An overview of the photometric systems is available here;
- A very usual is the Jonhson-Cousins (UBVRI) filters system
- Apparent magnitudes in the Jonhson-Cousin are noted with the capital letters of the filters: V for mV, U for mU, etc
Photometric systems
- Apparent flux of stars divide into three basic bands:
- UV (atm. cutoff at 0.32 μm),
- V (0.32–1 μm),
- IR (> 1 μm)
- Necessity to bring apparent magnitudes into physical units:
- Bring photometric measurements onto a standard physical flux scale;
- Remove atmospheric absorption
- Include wavelength-dependent calibration of the detecting device
- Photometric systems:
- Popular and early system: the Johnson-Cousins UBVRI system (Johnson 1966), normalized to Vega;
- Today, many photometric systems, adapted to different aims (for example, oriented towards certain types of stars such as cool stars)
- Questions:
- What are the precisions of the different photometric systems ?
- How to convert from one system to another ?
- How well can stellar atmosphere and radiative transfer models be used to devise photometric systems ?
3.4 From apparent magnitudes to flux
- Apparent magnitudes are related to Fν, in W m-2 Hz-1 (or A-1); in cgs units: erg s-1 m-2 A-1
Apparent magnitude at given wavelength as a function of flux density:
mλ = -2.5 log (Fλ/qλ)
- Expression of the flux: Fλ = qλ 10-0.4 mλ
- What are the qλ ? so-called zero-point values
- Question: how do we know the q's ? Answer: define absolute, or primary, standards.
- The q's correspond to the flux from a reference (primary or secondary standard) at wavelength λ
- The primary standards, hence the qλ, are defined in a given photometric system
- Useful references: Bessel 2005 (Annual Review of Astronomy and Astrophysics, ARAA), Hayes IAUS 1985
Flux calibration
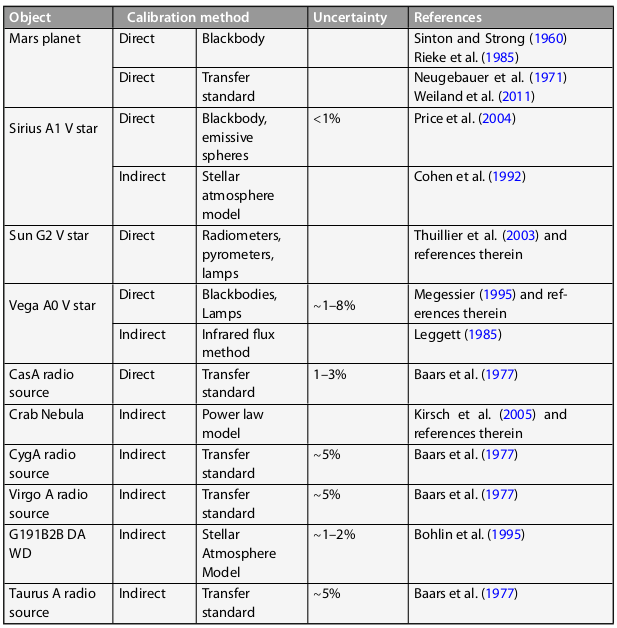
- Absolute, or primary standards;
- Secondary standards, defined against the primary standards (e.g. Landolt 1992)
- Absolute calibrations uses terrestrial standards (1000-2600K blackbody, tungsten striplamp, photodiodes), the Sun, primary and secondary stars
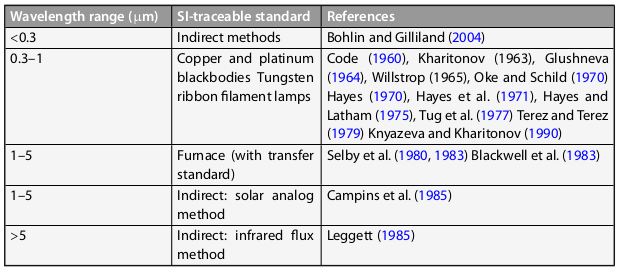
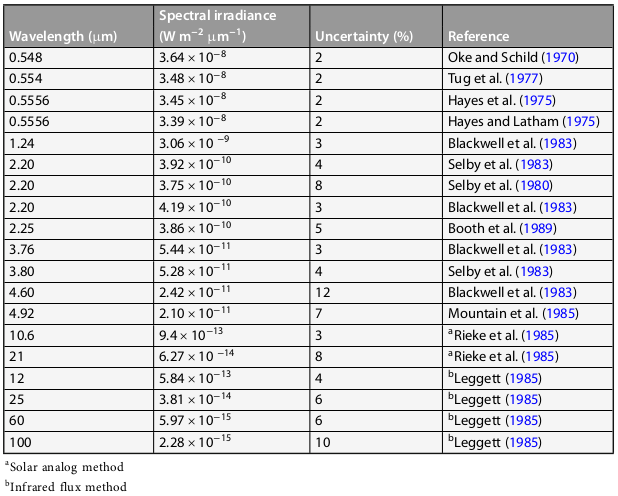
Usual primary standard star is Vega (α Lyrae, Teff=9550K, A0V, d=25 ly)
- qλ may be defined by many ways; for instance, such that color is uniformly zero (UBVRI), or such that mλ ≈ 0 for an ideal AOV in all filters (Vega system); in UBVRI system, V=0.03 for Vega such that m=0.03 in all bands (see Table)
⇒ Fν = FVega,λ 10-0.4(m-m0,λ)
- Relation between apparent magnitude and photon rates: \[ m_\lambda = m_{{\rm Vega},\lambda} -2.5 \log \frac{\int R \eta \lambda F_\lambda d\lambda}{\int R \eta \lambda F_0 d\lambda} \] with F0 the flux of Vega at λ.
Photometric precision and accuracy
- Photometric precision: typically few % (one speaks about "photometric nights")
- Current best precision photometric systems is 1 millimag; systematic errors in standard photometry is ≈ 0.01 mag, primarily because of poorly matched passbands, and limited sample of standard stars across the HR diagram;
- Uncertainties budget
- Absolute spectrum of Vega: 5% in the UV, 1.5% in V/NIR, 5-6% in IR
- Accuracy of the magnitude measured in a given photometry system
- Accuracy in the modeling of the photometric system used, ≈ 2%
Primary standards used in astronomy
The Vega magnitude system
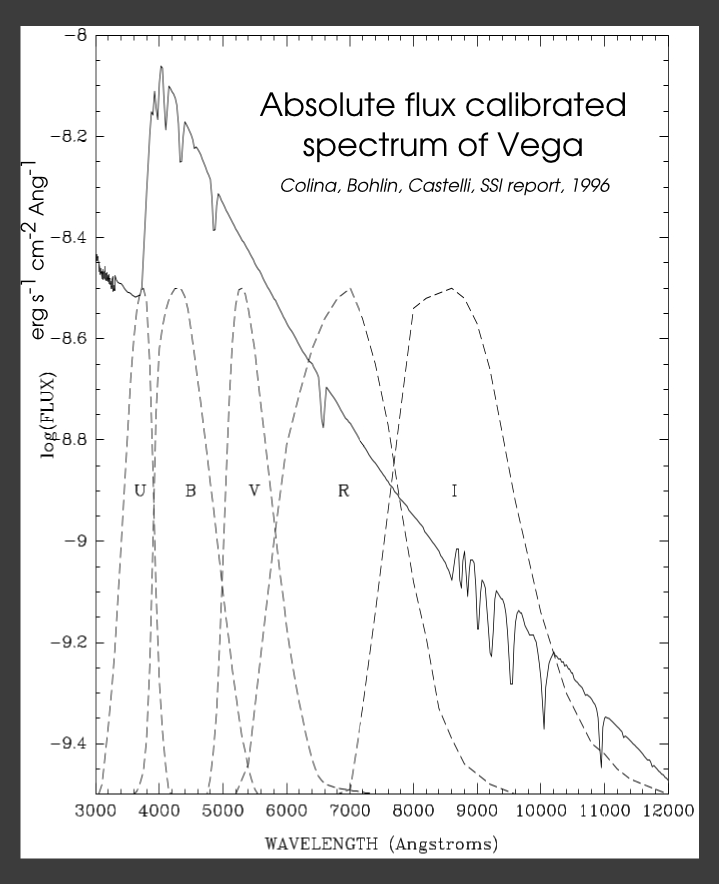
- αLyrae, Vega, one of the brightest stars in the night sky in the northern hemisphere; A0V
- In the Vega system, an ideal A0V has B=V=R=I=J=H=K=0, thus defining the zero-points of each bandpass
- In this system, Vega's magnitudes differ from 0 by ≈ ±0.1 mag
- see Hayes IAUS 1985 for V/NIR
- Different techniques for different λ
- Vega is the top-used primary standard (HST, Spitzer, SDSS)
- Not the only one: Sirius, the Sun (variable)
The Vega magnitude system
- Vega has been used as a primary since the 60s, thus enabling its flux to be measured from the UV (<0.3μm) to the near IR (>5 μm).
- Vega's monochromatic flux at 555nm: best value is 3.46(-11)±0.7% W m-2 nm-1 (Megessier 1995)
- Validity as a good primary has been questioned; dusty debry disk hence, extrapolation beyond 5μm risky; yet, if not variable, that's ok
The UBVRI magnitude system
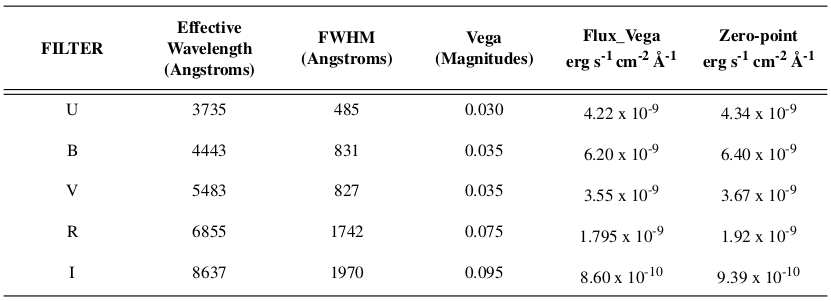
Questions:
- Can you recover the magnitudes of Vega in each band?
- What is the flux of a V=2 star ?
- Check that you can convert the flux from erg/s/cm2/ang into W/m2/nm
3.5 Bolometric magnitude
- Bolometric means 'integrated over all frequencies'; 'bolometers' are detecting devices which collect the electromagnetic radiation over a wide range of frequencies.
Bolometric magnitude is thus related to the total, or integrated, flux: F=∫ Fν dν
mbol = -2.5 log F + C
- Equivalently, the bolometric absolute magnitude is related to the total luminosity;
- Constant C is defined with respect to the Sun:
- mbol - mbol,\(\odot\) = -2.5 log(F/Fsun)
- Mbol - Mbol,\(\odot\) = -2.5 log(L/Lsun)
- Stellar luminosity covers a wide range of values:
- Brightest stars: ~106 \(L_\odot\), white dwarfs: ~10-3 \(L_\odot\), Brown dwarfs: ~10-7 \(L_\odot\);
- In practice
- bolometric magnitude is usually I+V+U (main input windows accessible from the ground)
- if one observes a star in a limited spectral range, how to correct for the missing flux? → bolometric correction
Bolometric correction
Bolometric correction (BC) = difference between the visual and bolometric magnitude:
BC = mbol - V
mbol = V + BC and also (show it) Mbol = MV + BC
- BC is always negative
- One expects that BC in the visual is minimum for stars with a spectral energy density peaking in band V; in contrast, BCV would be large for very hot, or very cold, stars. A natural choice for the zero-point of bolometric magnitude should thus be somewhere around F- or G-type stars.
- For the Sun, which is a G2 V star in the MK classification:
- BC\(_\odot\) = -0.08
- V=-26.75
- mbol,\(\odot\)=-26.75-0.08=-26.83
From absolute magnitude to luminosity
- Apparent magnitude: m related to Fν
Absolute blometric magnitude: M related to Lν
M = -2.5 log Fν(d0) + C, d0=10pc where Fν(d0) = Lν / 4π d02, is the flux density at a reference distance d0=10pc.
- Equivalently: M = 4.74 - 2.5 log (L/Lsun)
- \(L_\odot\) = 3.828×1033 erg s-1; \(M_{\rm bol,\odot}\) = 4.74
Warnings
- The value of mbol,\(\odot\) (or Mbol,\(\odot\)) is arbitrary; this is a zero-point value for the bolometric magnitudes, very much like the qλ for the magnitude scale. The value of mbol,\(\odot\) is thus a definition and is not a measurement.
- See this paper for a useful description and discussion.
- The value of BC\(_\odot\) can vary from -0.20 to -0.07; this depends upon the stellar models used to compute BC.
IAU 2015 Resolution B2: Mbol=0 corresponds to Lref=3.0128E28 W≈ 100Lsun, with Lsun=3.828E26 W, hence Mbol,Sun=4.74:
Mbol = 4.74 -2.5log(L/Lo)
- Translation to the apparent bolometric magnitude scale: mbol,ref=0 corresponds to Fref=Lref/(4π d02)=2.53E-8 W/m2; hence mbol,Sun=-2.5log(Fsun/Fref)=-26.83 (see above). In the UBVRI system, V=-26.75, hence BCsun=-0.08.
- There are tabulated bolometric corrections depending on the spectral type and luminosity class (see 3.6)
3.6 Color index
Definition:
color index = \(m_{\lambda_1} - m_{\lambda_2}\)
- Notation: U for \(m_U\), V for \(m_V\)
- V = mV = MV + 5 log(dpc) -5: apparent visual magnitude
- Color index: U-B, V-K, etc…
- ultraviolet minus blue color index: U-B = mU - mB
- blue minus visible: B-V = mB - mV
- Properties of color index:
- independent of distance (flux ratio) hence apparent or absolute magnitudes;
- shape of the stellar spectrum between two bands
- hot stars are blue: B-V \(<0\), \(\approx -0.3\)
- cool stars are red: B-V \(>0\), \(\approx 1.5\)
Values
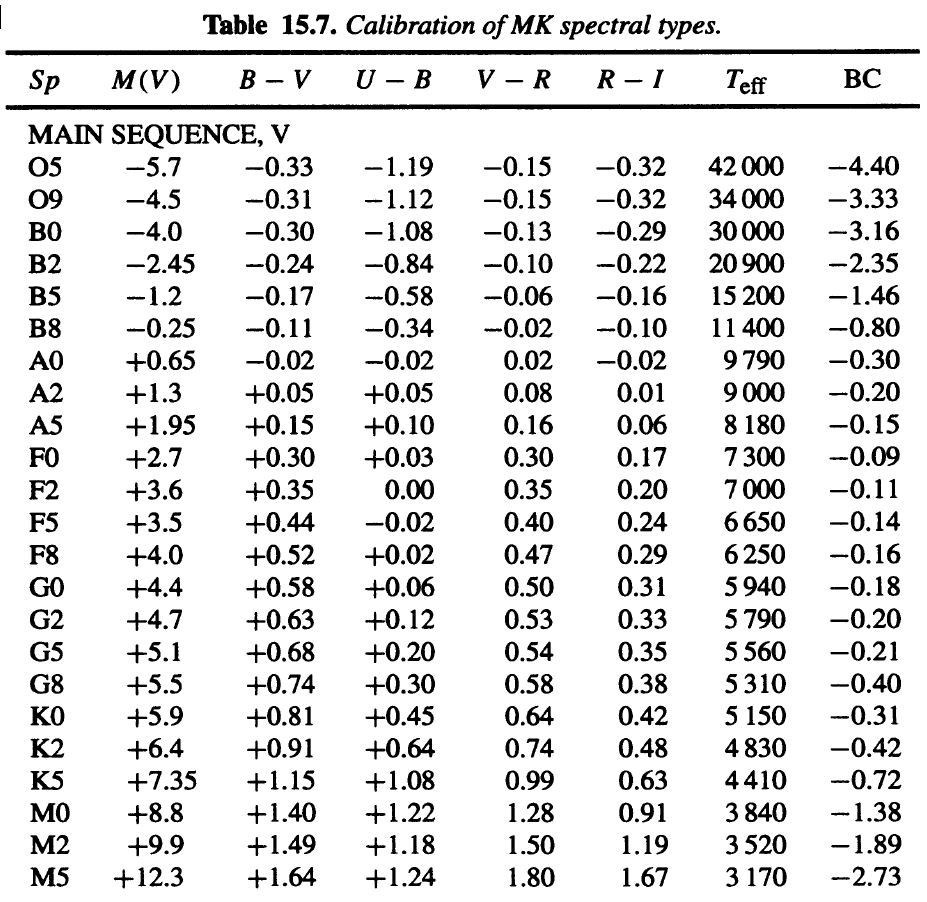
- Table from Allen, Astrophyiscal quantitities (4th ed. 2002)
- Color index in the UBVRI system: note that the color of a Vega-like star are ≈ zero, by construction
- Note that BC≈-0.20 for the Sun, in contrast with the -0.08 value quoted above, reflecting the underlying stellar models used to compute BC depending on the MK spectral types.
4 Exercises
Magnitudes
- The absolute magnitude of a given star is M; what is the apparent magnitude of this star at a distance d expressed in pc?
- The apparent magnitude of the Sun is V = -26.75; compute MV.
- From the CDS, Sirius magnitudes (in Johnson-Cousins system) are:
U: -1.51; B: -1.46; V: -1.46; R: -1.46; I: -1.43; J: -1.36;
H=-1.33; K: -1.35
- Compute U-B and B-V ? can you anticipate on the spectral type of the star ?
- Teff ≈ 10000 K: λmax ? consistent with color indices ?
- BC = -0.09: mbol = ?
- Absolute magnitude of Vega (d=25ly) in V band?
- Give an expression of the distance modulus as a function of the parallax p in mas.
- Show that the bolometric correction is the same for apparent and absolute magnitudes
Photometric systems
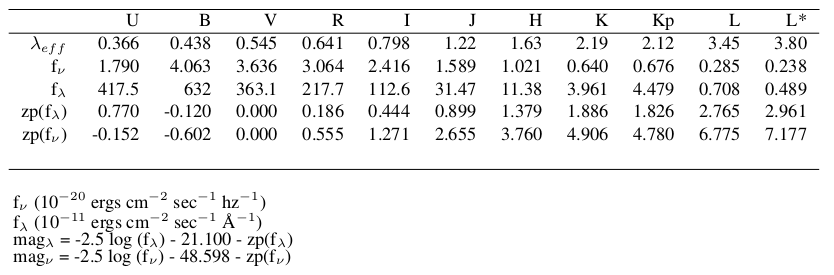
This Table (taken from Bessel et al 1998) gives, for a fictitious A0 star (based on synthetic photospheric spectrum) observed through the UBVRIJHKL Cousins-Glass-Johnson system, the effective λ of the filters, the absolute flux (corresponding to zero magnitude), and the zeropoint magnitudes.
- what is the flux, in the V band, of this A0 star? is this consistent with the values for Vega shown before?
- convert fλ into fν
- explain the offset values, 21.1 and 48.598, in the expressions of magν and magλ
- in this photometric system, what is the V-flux of V=2 star?
- compute the zp(fν) and zp(fλ). Comment?
Brightness, flux, and luminosity
- Based on the Table shown previously for the Vega system, show that the flux of Vega in the U band is 1964 Jy.
- Consider a star of radius R and specific intensity Iν:
- Compute the flux Fν measured at a distance d;
- From this, what is the flux at the surface of the star
- At large distances, show that Fν = ΩS Iν with ΩS the solid angle of the source
- Consider a star as a black-body of temperature Teff:
- compute the integrated flux at the surface of the star
- from this, obtain the total luminosity L as a function of Teff;
- show that L = 4π2 R2 I0; is this consistent with your previous result ?
Photon rates from a solar-type star Consider a star with Teff=5500K of radius R=7x108 m, located at a distance d=10 ly:
- Compute the brightness I100, I500, and I1000 of the star at 100, 500, and 1000 nm; give the results in S.I. units (which you have to explicit) and in MJy/sr;
- Compute the wavelength of the peak of Iν and Iλ; comment;
- Compute the fluxes incident on the detecting device at each of the above wavelengths;
- The fluxes are measured through filters centered at each λ, of equivalent width δλ=0.01λ; the detector has an efficiency η=80%; compute the power Pλ measured per unit area at the detector;
- Compute the corresponding photon rates Nλ
Proxima Centauri (α Cen C)

- From the CDS portal, find the parallax of Proxima Centauri
- What is the problem ?
- Check that the angular distance between the J2000 and ICRS coordinates is ≈ 60"
- Check that the distance along the RA and DEC axis are δ
x=-58.6" and δ y= 11.9"
Hint: the angular distance ψ between the two positions is:
cos ψ = sin(δ1)sin(δ2) + cos(δ1)cos(δ2)cos(α1-α2)
Galactic Infrared Emission
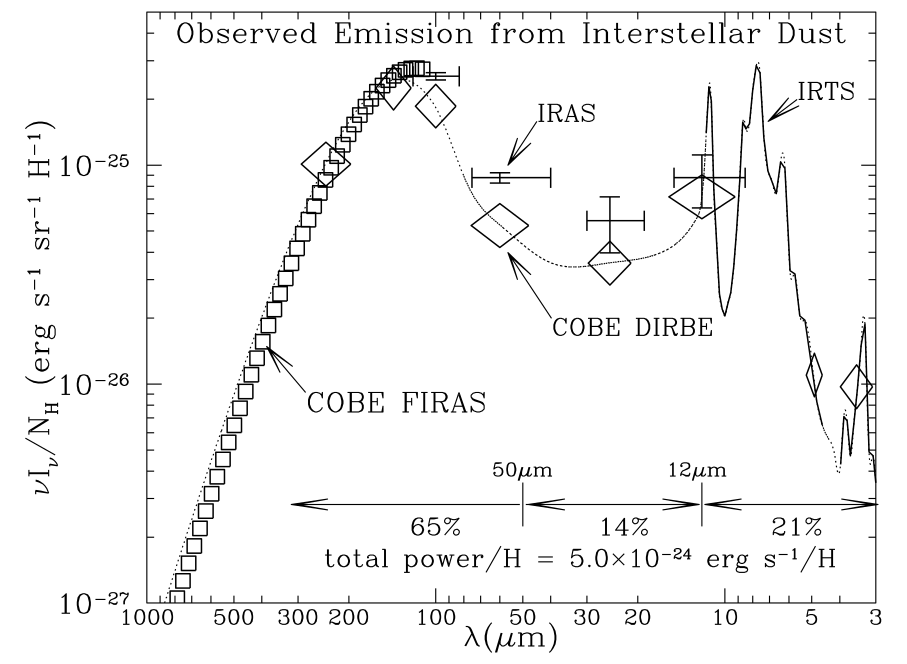
- At the bottom of the plot, the contribution to the total IR emission is indicated (in %)
- Make sure you understand the units of the plotted quantity;
- Can you recover the orders of magnitudes of these relative contributions ?
- Can you recover the total emission of 5x10-24 erg s-1 H-1
5 Radiation fundamentals
In defining the magnitude, we mentionned physical quantities such as the flux and luminosity without going in the details of how these quantities are defined. We now go into more details. In doing so, we will introduce a less familiar quantity, the specific intensity (also called brightness although this is a more ambiguous word and we prefer to call it specific intensity). In the process, we will review our knowledge of the black-body radiation which is so essential in astrophysics.
Definitions
- Luminosity: L or Lν
- Flux density: F or Fν
- Specific intensity (or brightness): Iν
5.1 Luminosity
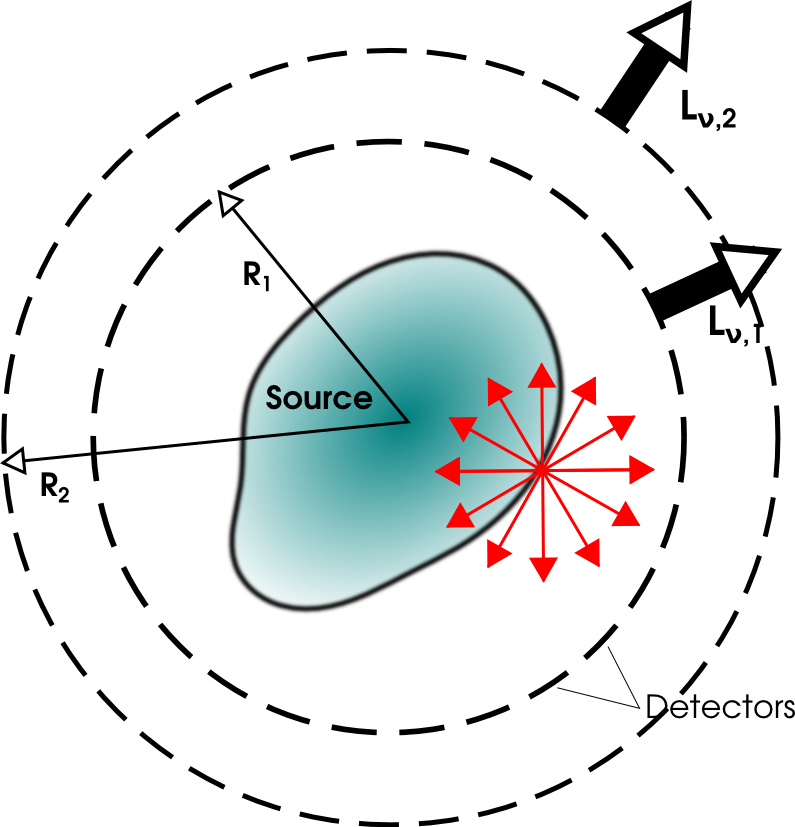
- This is an intrinsic property of a source
- Spectral luminosity Lν: total power per unit bandwidth emitted by the source, in W/Hz
- Energy conservation: Lν,1 = Lν,2
- Warning: Luminosity is rarely called luminosity, but more frequently flux
5.2 Specific intensity
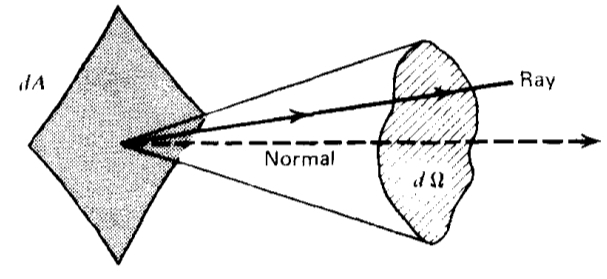
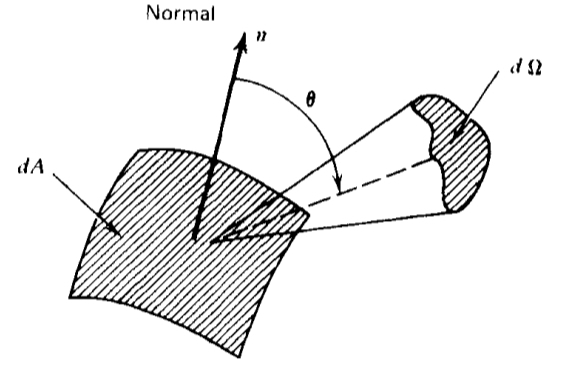
- Consider an area dA (e.g. your detector) embedded in a radiation field
- Energy flowing accross dA, carried by the bundle of rays within solid angle element dΩ, per unit time and frequency range ?
(1) direction is perpendical to dA:
dEν = Iν(θ,φ) dA dΩ dν dt
(2) direction makes an angle θ from the normal to dA:
dEν = Iν(θ,φ) dA⊥ dΩ dν dt
with dA⊥ = dA cos(θ)
- Total, or integrated intensity: I=∫ Iν dν
5.3 Flux density
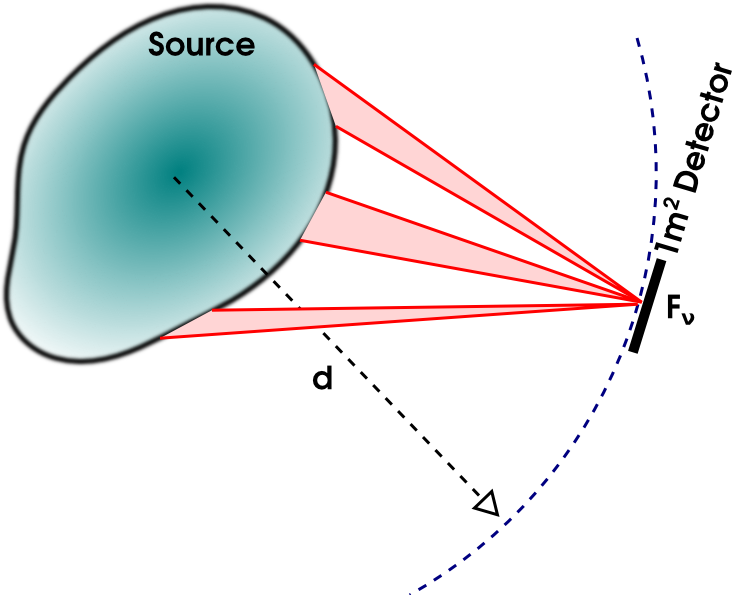
Expose an area dA to some radiation during a time dt. The energy in bandwidth dν crossing dA from all directions is:
Fν dA dt dν = ∫Ω dEν
- In terms of the specific intensity: Fν = ∫Ω Iν cos(θ) dΩ
- Units: Fν in W/m2/Hz
Detector of area 1m2 will intercept Fν W/m2/Hz from the source; obviously, the amount of energy depends upon the distance d:
Fν = Lν / [4 π d2], W m-2 Hz-1
- The flux density is not an intrinsic property of the source
Spatially resolved source: spectral flux density and specific intensity
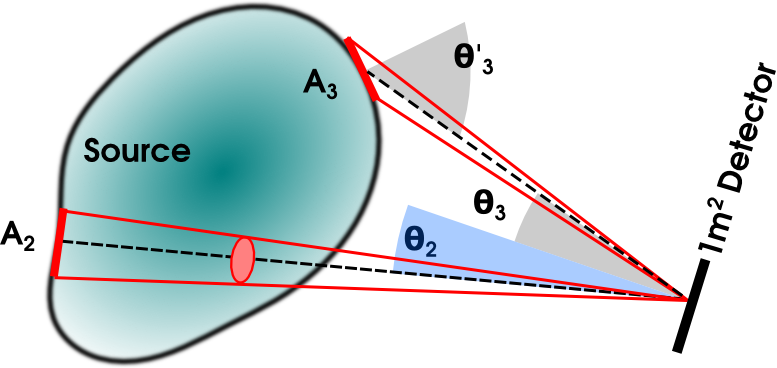
- Spectral flux density detected from \(A_k(\theta_k,\phi_k)\) within \(d \Omega(\theta_k,\phi_k)\): \[ d F_{\nu,k} = I_\nu(\theta_k,\phi_k) \cos\theta_k d \Omega(\theta_k,\phi_k) \]
- Total spectral flux density detected: \[ F_\nu = \int_{\Omega_S} I_\nu(\theta,\phi) \cos\theta d\Omega(\theta,\phi)\]
Units

- Iν is measured in W/m2/Hz/sr
- Fν is measured in W/m2/Hz
- More convenient unit is the Jansky (see black-body radiation)
- 1 Jy = 10-26 W/m2/Hz
- In cgs units: 1 J = 107 erg
- W/m2/Hz = 103 erg/cm2/Hz
5.4 Solid angles



- \(\Omega = S(d)/d^2 = \int\int d^2 S \vec{u}\cdot\vec{N}/d^2\)
- dΩ = dS cosα/d2
- Spherical coordinates: dΩ = sinθ dθ dφ
- Uniform sphere: Ω=4π
- Cylindrical cone of half-opening angle α: Ω=2π(1-cosα)≈πα2 for α≪1
Application
- Isotropic radiation field:
- Fν = ∫Ω I cos(θ) dΩ
- dΩ = sin(θ)dθ dφ
- F=0
- Integrating over one half:
- \(F_\nu = \int_0^{\pi/2} d\theta \int_0^{2\pi} d\phi I_\nu \cos(\theta)\sin(\theta) d\theta d\phi = \pi I_\nu\)
- Flux emitted by a star within solid angle ω is: Lν =
ω d2 Fν, where Fν is the flux density at a distance
d;
- The total luminosity Lν is thus (assuming it is isotropic) 4π d2 Fν
5.5 Fundamental properties of the specific intensity
How is Iν related to the radiation field emitted by the source?
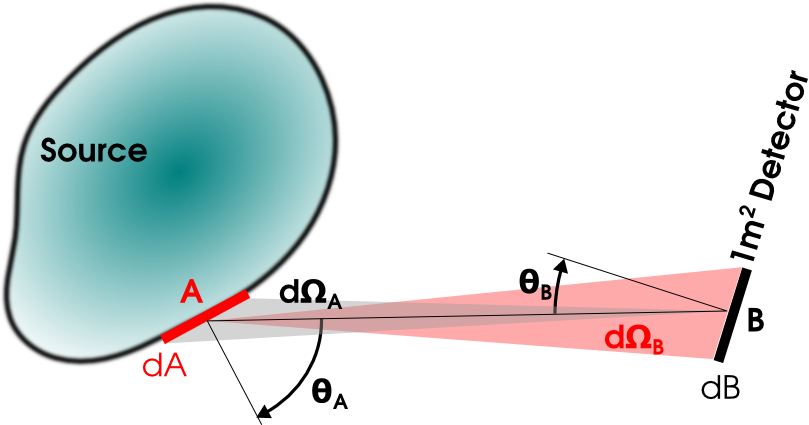
- \(d\Omega_A = dA_\perp /d^2\): \(dA_\perp = d A \cos\theta_A\)
- \(d\Omega_B = dB_\perp/d^2\): \(dB_\perp = d B \cos\theta_B\)
- pνA: power emitted by dA and crossing dB = Iν(A) dA⊥ dΩB
- pνB: power flowing through dB looking at dA = Iν(B) dB⊥ dΩA
- Assuming propagation in empty space: pνA=pνB
- Iν(A) = Iν(B): the detector measures the specific intensity emitted by the source; intrinsic property of the source
- Important: \(I_\nu\) can only be measured for spatially resolved sources
Conservation of the specific intensity (2)
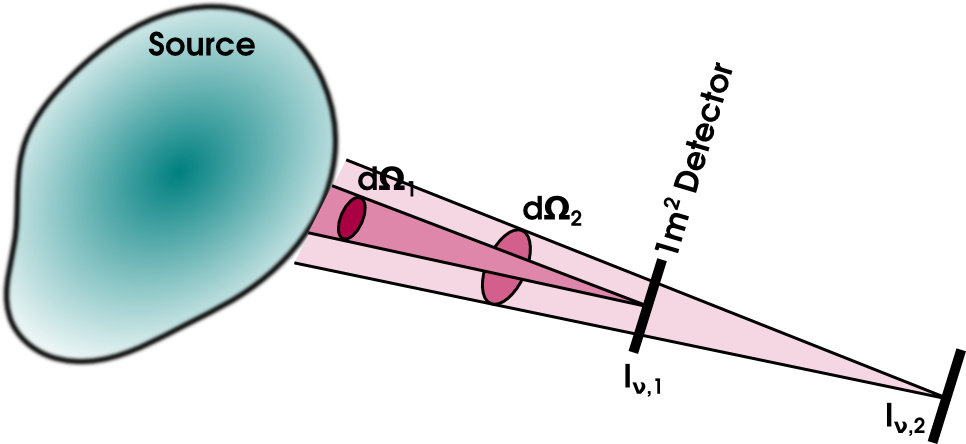
- \(I_{\nu,1}\): specific intensity measured on the detector at distance \(d_1\)
- \(I_{\nu,2}\): specific intensity measured on the detector at distance \(d_2\)
- Source area increases as \(d^2\) while dΩdet decreases as \(d^{-2}\)
- Conservation of energy in free space: \(I_{\nu,1} = I_{\nu,2} = I_\nu\)
- The detector measures the source brightness: Intrinsic property of the source
Resolved vs unresolved source
- Flux dilution when source becomes unresolved: specific intensity can only be measured for a resolved source unless its angular size (solid angle) is known;
- In contrast, if we do not know the source size, what we measure is the flux Fν;
- More generally, for an unresolved source, one measure the flux; if the distance is known, the luminosity is recovered; if in addition the source size is known, one obtains the specific intensity.
5.6 Spectral Energy Density (SED) and Reduced Brightness
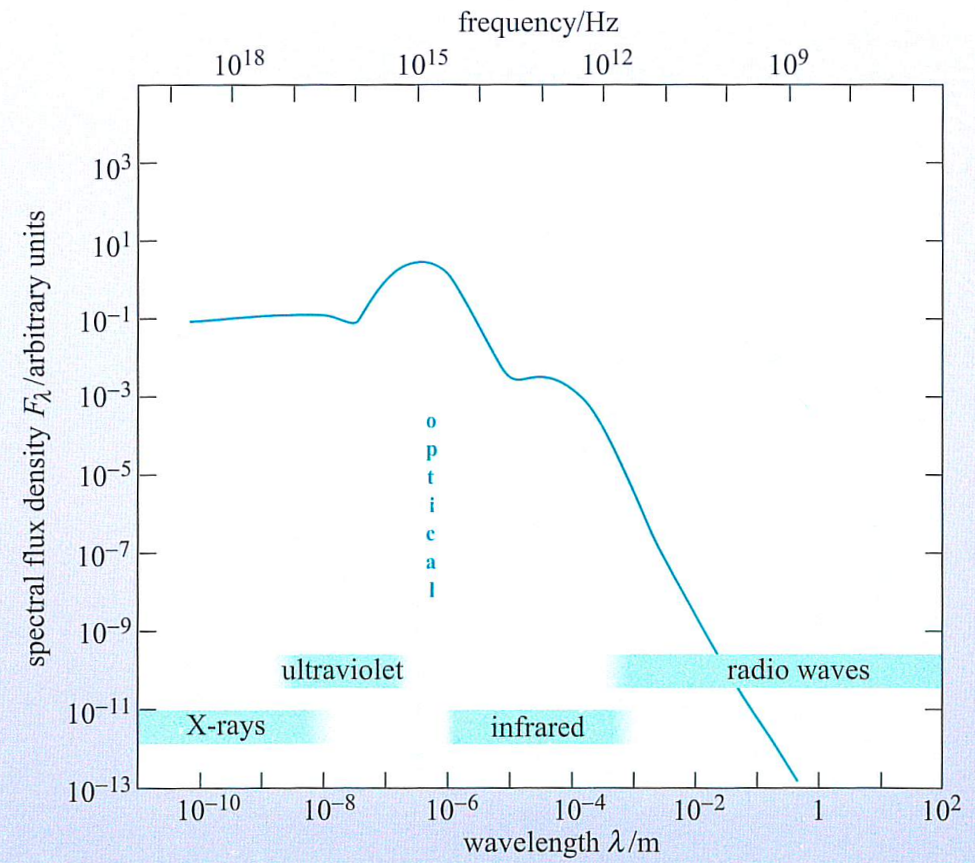
- SED: flux, or brightness, over a broad spectral range; here: sketch of the SED of a normal spiral galaxy
- This plot gives the sensation that the galaxy emits much more energy in the X-ray domain than in the radio domain.
- This is because the wavelength are shown on a logarithmic scale. However, displaying it on a linear scale would completely wash out the spectral details at short wavelength.
- Very broad spectrum: distortion of the spectrum: 1μm in the radio is tiny, but huge at short visible wavelenghts; Fλ will under-represent the flux emitted at radio wavelength, and overrepresent the flux at short wavelength.
Reduced brightness


- A very practical way to deal w/ this is to keep plotting the wavelength on a logarithmic scale, while replacing the flux Fλ by λ Fλ;
Using the reduced brightness also preserves the link between the area under the curve and the corresponding integrated energy:
\[ \int I_\nu d\nu = \int I_\lambda d\lambda \] and \[ \int \nu I_\nu d(\log\nu) = \int I_\nu d\nu \] so that also \[ \int \nu I_\nu d(\log\nu) = \int \lambda I_\lambda d(\log \lambda) \]
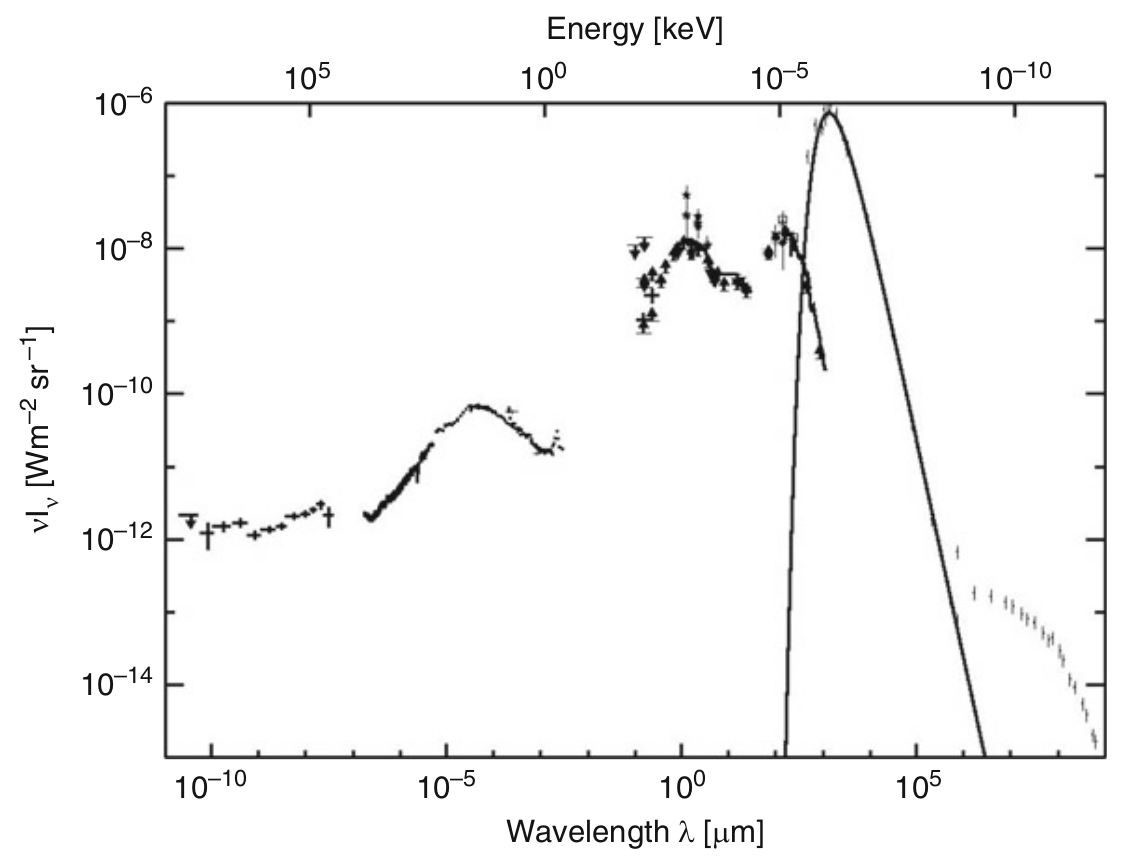
- Sky background radiation (zodiacal light subtracted); notice the CMB black-body
- By plotting ν Iν againt log(λ), it is possible to 'measure' directly, w/ a ruler, the area under the curve to obtain the energy radiated within a given spectral range.
6 Black-body radiation
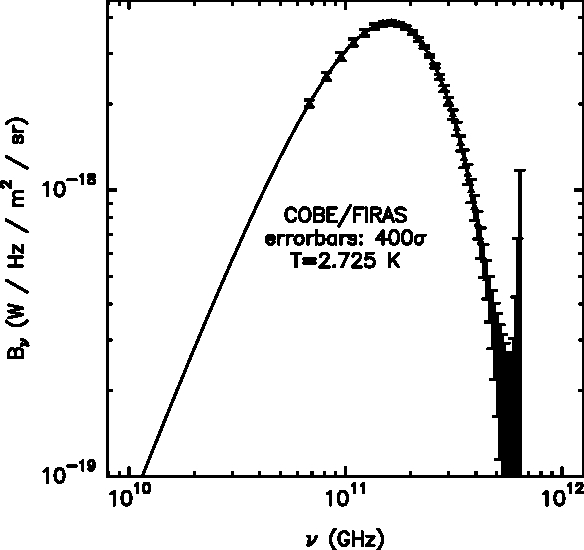
- The Cosmic Microwave Background (CMB)
- Notice the 1σ error bars which were multiplied by 400
The CMB in other units

- 1 Jy = 10-26 W/m2/Hz
6.1 Definition
- A black-body is an ideal body which absorbs 100% of the radiation regardless of the wavelength, incidence angle; the black body has zero reflectance and zero transmittance;
- Black-body radiation does not depend upon its geometry
- It is unpolarized
- Its specific intensity depends on a single parameter: the temperature
6.2 Mathematical expression
- The spectra interval may be frequency or wavelength
- Conservation of energy ensures that Bν dν = Bλ dλ
Two equivalent formulations:
\[B_\nu = \frac{2h\nu^3}{c^2}\,\left(e^{h\nu/k_BT}-1\right)^{-1}\]
abd
\[B_\lambda = \frac{2hc^2}{\lambda^5}\,\frac{1}{e^{hc/\lambda k_BT}-1}\]
6.3 Exercise
Do stars really radiate as a blackbody ?

- Absorption by atoms in the photosphere (H, H\(^-\))
- High abundance of metals in Pop I stars: absorption (lower right)
- Different elements trace differents heights hence diff. Teff
Do stars really radiate as black-bodies?

Can you recover the straight line in this plot? (Hint: use Wien's law)
7 Extinction
Light propagating through a medium suffers scattering (redistribution in phase and/or frequency) and absorption (opacity):
scattering + absorption = extinction
- Note: albedo ω=Csca/(Csca + Cabs)=Csca/Cext
- Absorption: Iλ = Iλ,0 exp(-τλ); τλ is the opacity at λ
- There is also emission by the medium itself
- Radiative transfer: solve emission + extinction processes
- In this Section:
- Atmospheric absorption
- Interstellar extinction by dust
7.1 Reflection nebulae


M78
M45 (Pleiades)
Interstellar clouds near bright stars; blue nebulosity is light scattered by dust; dark lanes are due to absorption;
7.2 Atmospheric absorption
- Different processes:
- scattering: light pollution
- refraction: λ-dependent light deviation
- turbulence: degrades the spatial resolution
- thermal emission: significant contribution at IR and mm
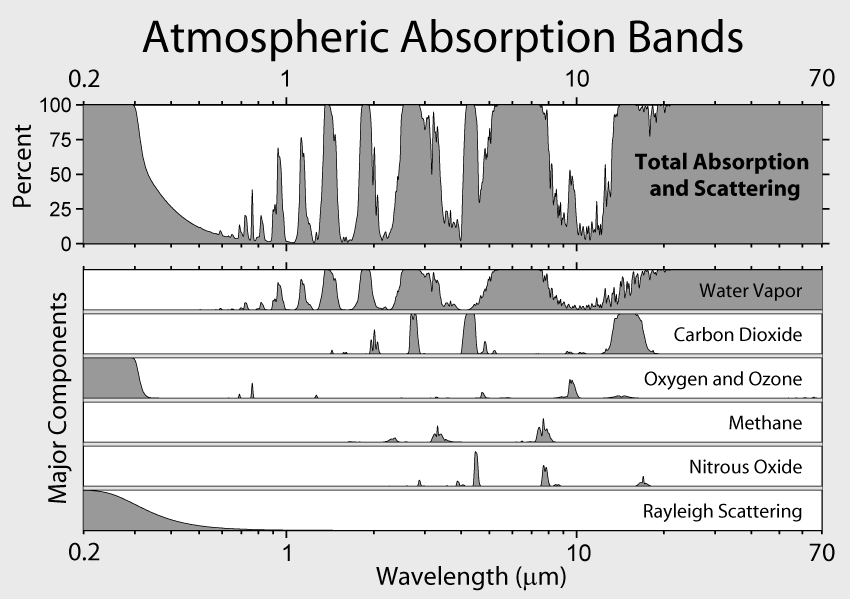
- Atmospheric windows: outside the windows, atm. absorption is very
strong; associated with absorption lines (O2, O3, CO2) or
continuum (UV)
- electronic (atomic, molecular) transitions: O, N, CH4, CO, H2O, O2, O3
- ro-vibrational and pure rotation lines: CO2, NO, CO, H2O, O3
- Chemical composition of the atm. is ≈ constant up to ≈ 90 km
- Hydrostatic scale height H≈8 km
- CO2: mid infrared absorption
- Airmass: 1/cos(z) = 1/sin(El) (approximation valid down to El≈20o)
7.2.1 Atmospheric windows

7.2.2 Atmosphere absorption
7.2.3 Why are observatories in altitude ?

- mixing ratio: r(z) = mass of water per vol. / mass of air per vol;
- rapidly varying function of altitude z
- quantity of precipitable water: the column density of water molecules above the observatory: \[ w(H2O) = \int_{z_0}^\infty n(H2O) dz \] and n(H2O) [cm-3] = 4.3x1025 P/P0 T/T0 r(z)
- typical values of w(H2{})) are 0 to a few mm;
Atmosphere windows in the mm and sub-mm

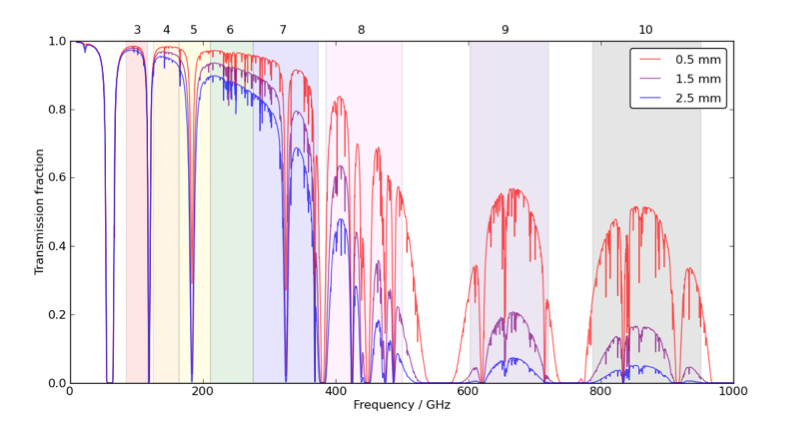
Left: NOEMA site (2 km); Right: ALMA site (5 km)
7.3 Interstellar extinction
Space absorption correction
- Extinction of light on the way from the source to the atmosphere
Positive correction to the apparent magnitude: A
M = m + 5 -5log10 dpc - A = m - DM - A
- Extinction or reddening (in magnitudes):
- Fλ,0: the un-reddened flux
- Aλ = 2.5 log10 (Fλ,0/Fλ)
- wavelength dependent: extinction curves
Aλ is proportional to the opacity τλ:
Aλ = 2.5log10 [exp(τλ)] = 1.086 τλ
- In band V, extinction is essentially due to interstellar dust
7.3.1 Reddening and colour excess
- Reddening: E(B-V) = AB - AV
- Aλ: reddening at one wavelength
- Other usual quantity: Aλ-AV = E(λ-V)
- By definition: M=m-DM-A, or m=M+DM+A
Color index: B-V = MB - MV + AB - AV
B-V = (B-V)0 + E(B-V)
- (B-V)0: intrinsic colour
- E(B-V) = AB-AV: colour excess
- Extinction curves: relative colour excess vs wavelength
- Usual quantities in ordinate: Aλ/E(B-V) or Aλ/AV, etc…
Important relation that you must know (Bohlin+78):
NH [cm-2] = 5.8 x1021 E(B-V)
7.3.2 Extinction curves: line-of-sight variability
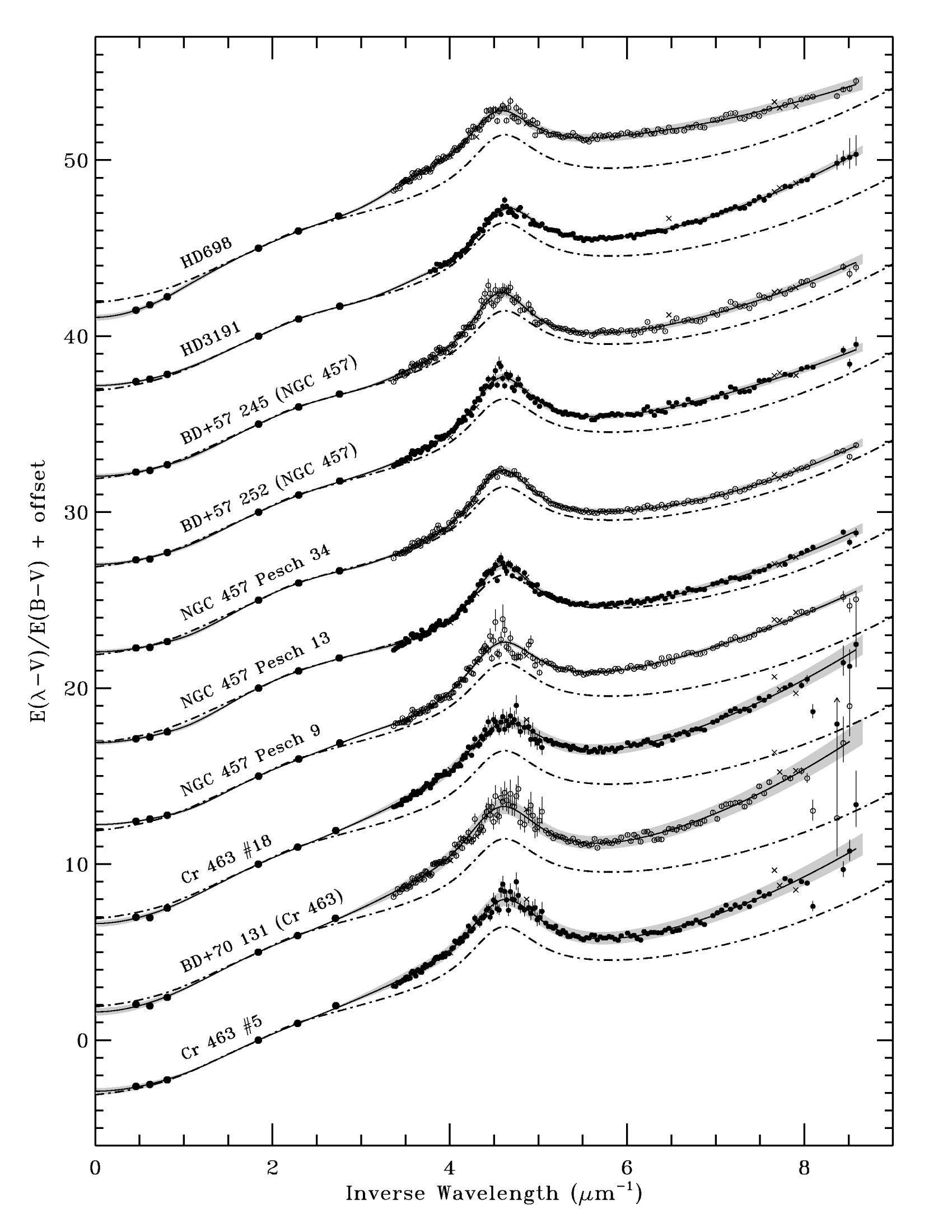
- Fitzpatrick & Massa 2007
- What is traced is (Aλ-AV)/(AB-AV)
- Note the similarity of all extinction curves: increase with λ-1, and the bump at 4.5μm-1
- Note also that there are differences
7.3.3 Interstellar extinction curves: common features
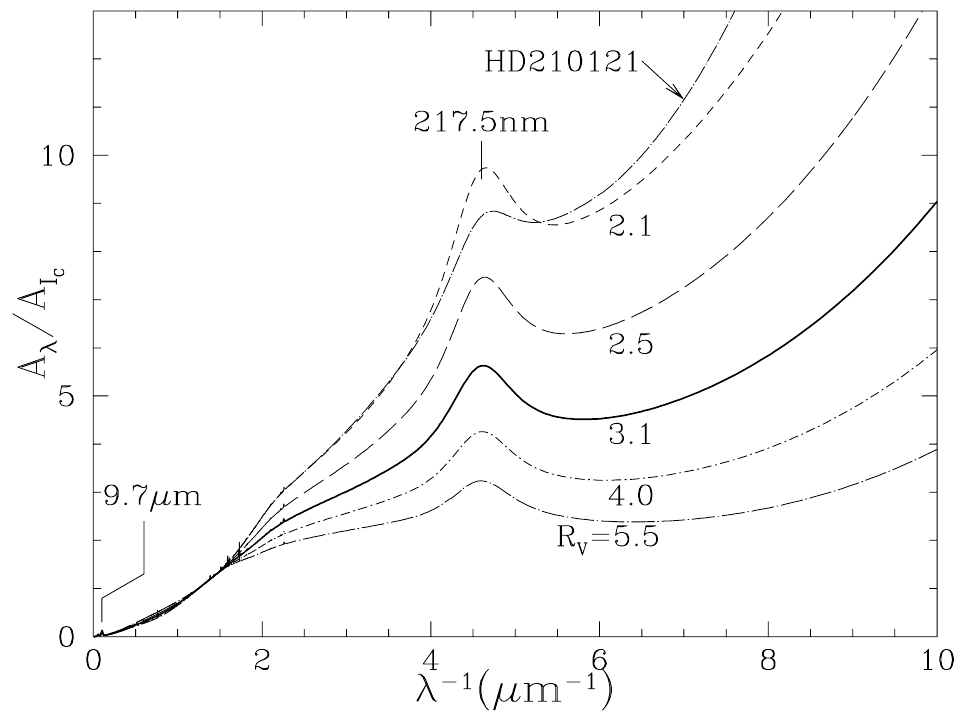
- Extinction curve: Aλ/E(B-V) or Aλ vs λ
- Here, what is traced is: Aλ relative to extinction in the Cousins I band (8020\(\mathring{A}\))
- Extinction increases with decreasing λ
- More extinction at blue wavelength: reddening
- Different curves for different lines of sight
- RV: total-to-selective absorption
- RV = AV/E(B-V) = AV/(AB-AV): depends on dust composition and size, hence on the line-of-sight
- RV ≈ 3.1, on average in the diffuse ISM in the MW
Exercise: show the important relation \[ A_\lambda = E(\lambda - V) + R_V E(B-V) \]
7.3.4 Reddening laws: the Cardelli+89 paper
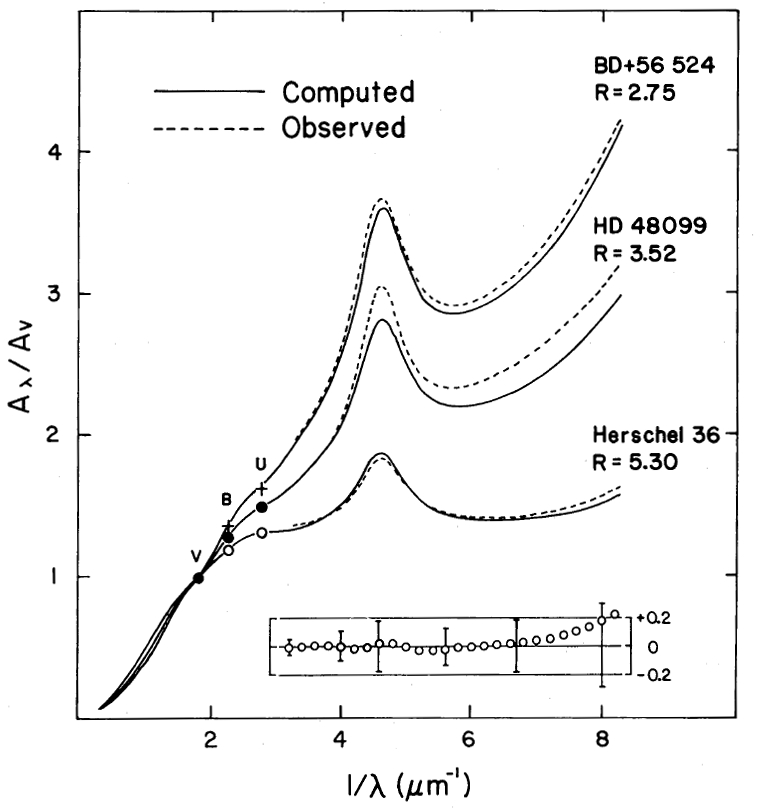
- Trace A(λ)/AV curve instead of E(λ-V)/E(B-V)
Average A(λ)/AV curve, for 0.125≤λ≤3.5 mic, parameterized by RV=AV/E(B-V), applicable for dense and diffuse ISM:
Aλ/AV = f(λ;RV) = a(x) + b(x)/RV, x=1/λ[mic-1]
- See also Fitzpatrick+07
7.3.5 Interstellar extinction curves: dust size

- Dust grains must be small:
- large grains would be in the geometric optics limit, hence λ-independent extinction cross-section
- variations of Aλ down to λ=0.1 mic implies that there must be small grains: 2πa≤ λ
- Implise that a significant population of grains with a≤0.015mic must be present
7.3.6 Source variability: grain growth

- Cardelli+89
- A(λ)/AV instead of E(λ-V)/E(B-V)
- Total-to-selective extinction: RV = AV/E(B-V)≈ 3.1 on average in the Galaxy
- Flattening of the curve:
- signature of grain growth
- large grains: Aλ ind. of λ, RV → ∞
- dense clouds: RV=4-5
7.3.7 Digressions
The 2175 angstrom feature

- conspicuous feature at λ-1 = 4.6 micr-1 or 2175 angstrom
- strong feature: must be an abundant material, hence made of the most abundant elements
- variable width
- sp2-bond of carbon in carbon sheets (graphite): PAHs best candidates, but still elusive
Diffuse Interstellar Bands
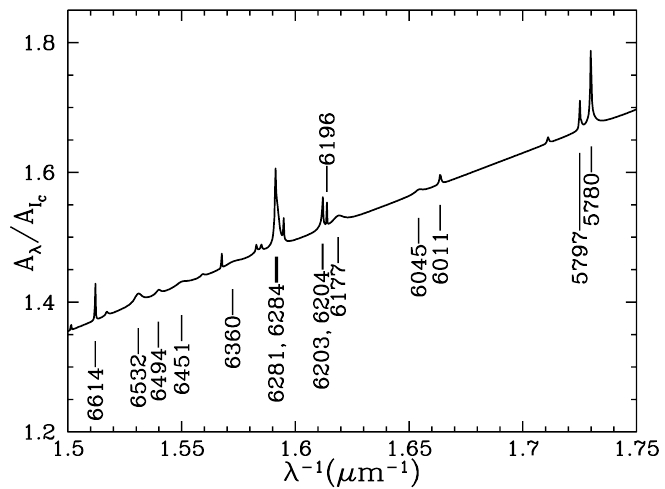
- Carriers are unknown
- Free-flying (large) molecules or ultra-small dust grains
- fine-structure spectral features (molecular rotation ?)
- As of today, still an open question