Pierre-Yves Longaretti
pyl at
obs.ujf-grenoble.fr
IPAG (Institut de Planétologie et d'Astrophysique de Grenoble)
BP 53
38041 Grenoble Cedex 9
BP 53
38041 Grenoble Cedex 9

Menu:
Research: accretion in astrophysical disks
Accretion disks are nearly ubiquitous in astrophysics; they are commonly directly observed or indirectly inferred around Young Stellar Objects (YSOs), at the center of Active Galactic Nuclei (ANGs), in micro-quasars, etc. Their life-times, as constrained by observations, are extremely short in comparison with the evolution times that microphysical (e.g. collisions between gas particles) can produce. To accommodate such short evolution time scales, some very efficient physical processes must be at work in the disks, to remove angular momentum from the disk to allow its material content to accrete fast enough on the central object.
The most popular mechanism that has been proposed to date is disk turbulence, and my research on this theme has focused on the analysis and characterization of turbulent processes. I have looked to date at two of the most widely discussed turbulence generation processes, and characterized their transport efficiencies.
The shearing box setting:
Most studies of turbulence in disks look at a small patch of the disk in which the disk curvature is ignored as well as the variation of the shear and of the rotation across the box. This is a consequence of the very large resolutions required by simulations to achieve sufficiently precis results in the determination of the turbulent transport efficiency. A mean magnetic field can be added to the box, as well as vertical stratification. In the simplest versions, the boundary conditions are periodic in the azimuthal and vertical directions, and shear-periodic in the radial one (i.e., periodic after the relative motion of the two boundaries due to the mean shear has been substracted out).
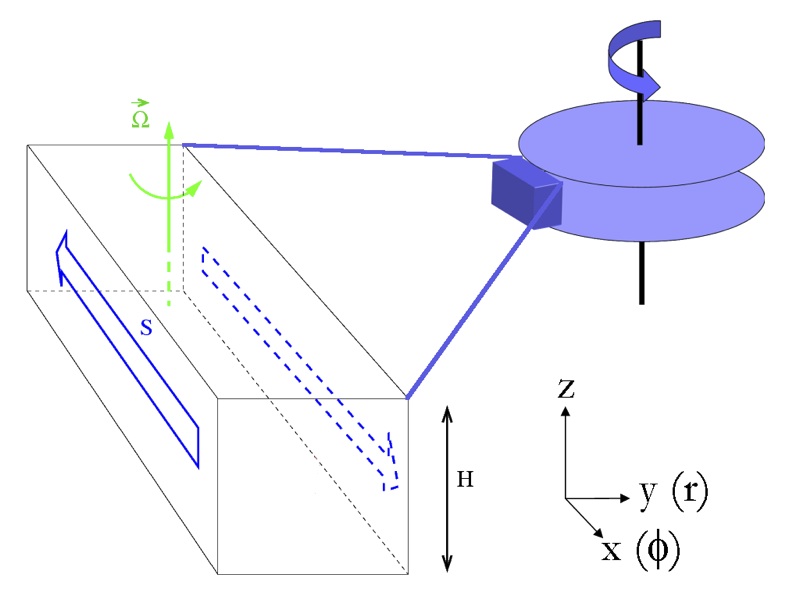
Magneto-rotational instability (MRI):
The MRI is by now the most popular turbulence-generating process in accretion disk theory. It is very generic as it requires only some magnetic field to be present in the disk, and the angular velocity of the disk to be decreasing outwards, to conditions that can hardly be not satisfied in actual disk systems.
The following figure shows one magnetic field component in a typical state in a 4:4:1 one shearing box:

My first piece of work on this topic was performed in collaboration with Geoffroy Lesur. We showed that the angular momentum transport efficiency - a process controlled by the flow large scales - was substantially dependent on the flow dissipation processes that operate at the small-scales of the flow:
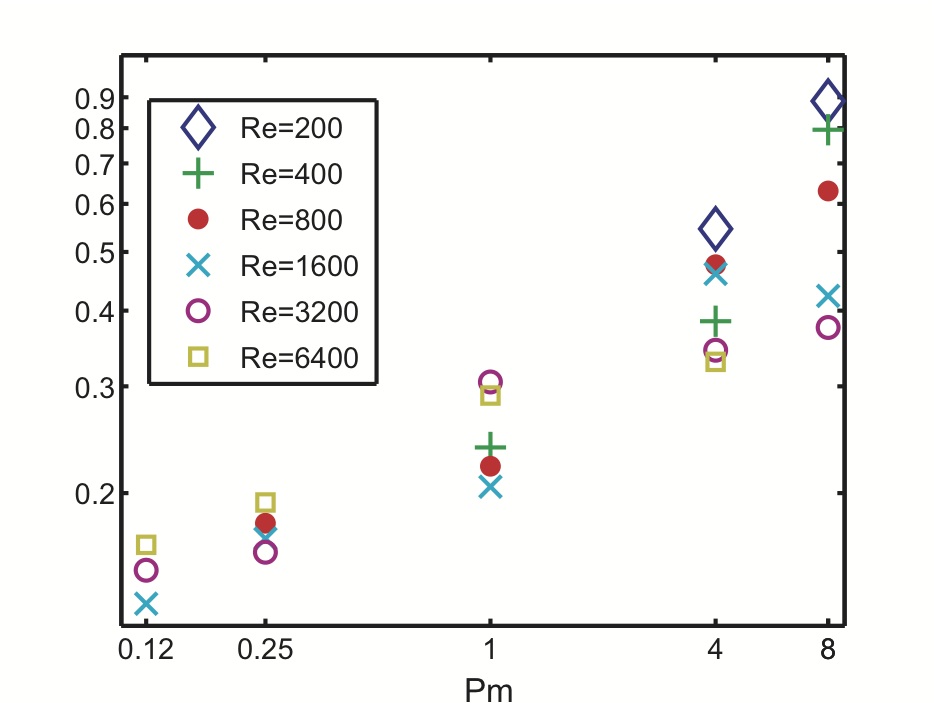
Transport as a function of the magnetic Prandtl number Pm. Pm is
the ratio of the disk viscosity to its resistivity
In a
more recent reinvestigation, we have shown that for small magnetic
Prandtl numbers Pm (Pm being the ratio of the visocisity to the
resistivity) the angular momentum transport is in fact controlled by
the fluid resistivity:
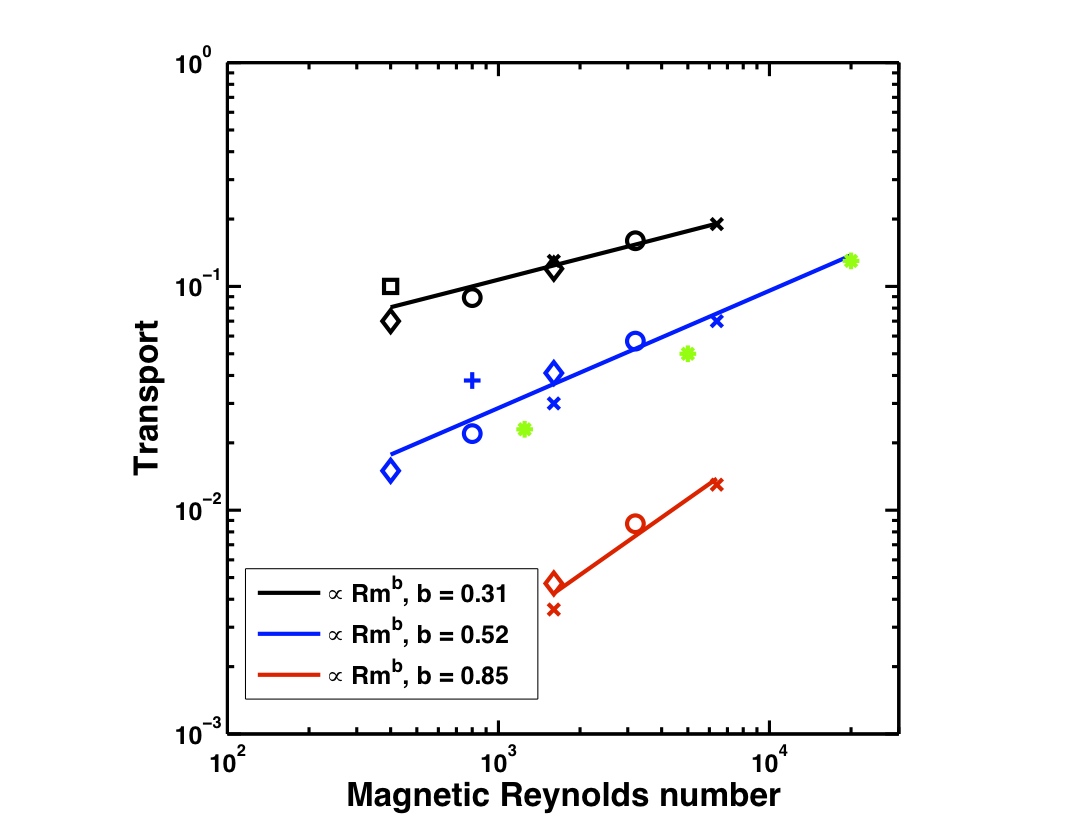

The origin of this behavior is still
unknown and has been the object of a number of speculations.
We have also investigated the transport of the magnetic field by the MRI, and found that it was closely related to the momentum transport.
Our recent investigation has focused on the direction of transfers in Fourier space. We showed that it is always direct, so that the dependence of MRI transport on microscopic dissipation is not due to information flowing from small to large scales. The explanation lies instead in the long-range in scales of kinetic-magnetic energy exchanges.
References:
Lesur & Longaretti, MNRAS, 2007
Lesur & Longaretti, A&A, 2009
Longaretti & Lesur, A&A, 2010
Lesur & Longaretti, A&A, 2011
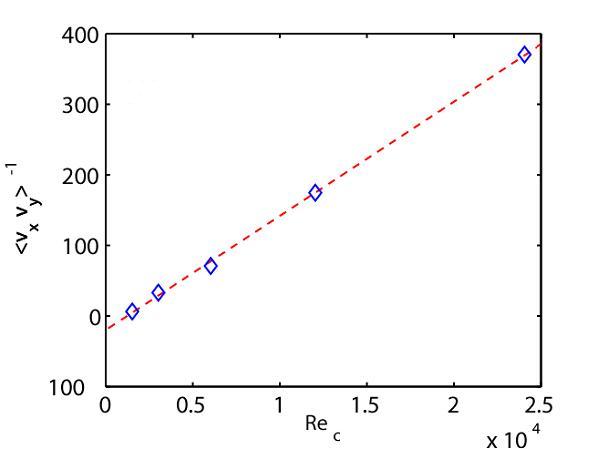
For a number of decades it was pointed out that the Reynolds number of astrophysical disks being astronomically large, they were bound to be turbulent even if they are linearly stable (i.e. subcritical). An unmagnetized, unstratified shearing box is a simple model satisfiying the subcriticality requirement. This process has been highly debated, as the transition to turbulence was not observed in simulations in disk-like settings. By reinvestigating this process in collaboration with Geoffroy Lesur we found that it was possibly present in keplerian-like flows, but extremely inefficient due to the steep correlation of transport with the laminar-turbulent transport transition Reynolds number, a feature that has a simple physical explanation:
We have also investigated the transport of the magnetic field by the MRI, and found that it was closely related to the momentum transport.
Our recent investigation has focused on the direction of transfers in Fourier space. We showed that it is always direct, so that the dependence of MRI transport on microscopic dissipation is not due to information flowing from small to large scales. The explanation lies instead in the long-range in scales of kinetic-magnetic energy exchanges.
References:
Lesur & Longaretti, MNRAS, 2007
Lesur & Longaretti, A&A, 2009
Longaretti & Lesur, A&A, 2010
Lesur & Longaretti, A&A, 2011
Subcritical turbulence:
For a number of decades it was pointed out that the Reynolds number of astrophysical disks being astronomically large, they were bound to be turbulent even if they are linearly stable (i.e. subcritical). An unmagnetized, unstratified shearing box is a simple model satisfiying the subcriticality requirement. This process has been highly debated, as the transition to turbulence was not observed in simulations in disk-like settings. By reinvestigating this process in collaboration with Geoffroy Lesur we found that it was possibly present in keplerian-like flows, but extremely inefficient due to the steep correlation of transport with the laminar-turbulent transport transition Reynolds number, a feature that has a simple physical explanation:

References:
Longaretti, ApJ, 2002
Longaretti & Dauchot, 2005 (IUTAM Symposium on laminar-turbulent transition and finite amplitude solutions)
Lesur & Longaretti, A & A, 2005
See my publication list
Longaretti, ApJ, 2002
Longaretti & Dauchot, 2005 (IUTAM Symposium on laminar-turbulent transition and finite amplitude solutions)
Lesur & Longaretti, A & A, 2005
Other or older work
See my publication list